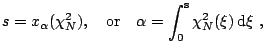Chi-square test
If N measurements yi are compared to some model or theory predicting values gi, and if the measurements are assumed normally distributed around gi, uncorrelated and with variances 
, then the sum
follows the 
(chi-square) distribution with N degrees of freedom. The test compares s with the integral of the distribution; if the sum above is equal to the quantile 
of the distribution
then the probability of obtaining s or a larger value in the 'null hypothesis' (i.e. the yi are drawn from a distribution described by the 
) is given by 
.
Integral curves for the distribution exist in computer libraries or are tabulated in the literature. Note that the test may express little about the inherent assumptions; wrong hypotheses or measurements can, but need not cause large 's. The only statement to make about a measured s is the one above: `` is the probability of finding a as large as s or larger, in the null hypothesis.
Rudolf K. Bock, Oct 2000
 |
